مفاهیم دنباله های حسابی و هندسی پایه دهم با نمونه‌ سوال‌های جذاب

دنباله های حسابی و هندسی پایه دهم از مهم‌ترین مباحث کتاب ریاضی دهم است. یادگیری دقیق این موضوع باعث می‌شود دانش‌آموزان بتوانند بسیاری از تمرین‌ها، مثال‌ها و حتی سؤال‌های امتحانی و تستی را راحت‌تر حل کنند. این مبحث فقط در سال دهم کاربرد ندارد؛ بلکه پایه‌ای برای فهم مفاهیم پیشرفته‌تر ریاضی در سال‌های بعد نیز محسوب می‌شود. به همین دلیل تسلط بر دنباله های حسابی و هندسی پایه دهم برای موفقیت تحصیلی بسیار ضروری است.

دنباله‌ها به ما کمک می‌کنند الگوهای عددی را بهتر بشناسیم، روابط بین اعداد را تحلیل کنیم و با استفاده از یک قاعده مشخص، اعضای بعدی یک رشته عددی را پیدا کنیم. در این مقاله تلاش کرده‌ایم با توضیحی کاملاً ساده و قابل‌فهم، به همراه مثال‌های کاربردی، به شما کمک کنیم دنباله‌ های حسابی و هندسی را در کوتاه‌ترین زمان یاد بگیرید و از آن در حل مسائل استفاده کنید.

آموزش دنباله های حسابی و هندسی پایه دهم

قبل از شروع هر درس جدید، بهتر است خودتان را ارزیابی کنید تا ببینید مفاهیم لازم را از قبل یاد گرفته‌اید یا نه. یکی از این مفاهیم دنباله‌ها هستند.

دنباله چیست؟
دنباله همان الگوی عددی است که قبلاً هم با آن آشنا شده‌اید؛ یعنی مجموعه‌ای از عددها که با یک قانون مشخص پشت سر هم نوشته می‌شوند.

به مثال زیر توجه کنید:

…, 12, 10, 8, 6, 4, 2

این یک دنباله است. جملهٔ اول آن ۲ است. جملهٔ دوم آن ۴ است و جملهٔ ششم آن ۱۲ است.

تصویر زیر نیز یک دنباله یا یک الگوی هندسی را نشان می دهد:

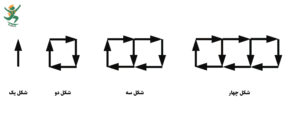
در پایه‌های قبلی یاد گرفته بودید که چگونه با پیدا کردن رابطه الگو می‌توانید جمله‌های بعدی را هم به دست آورید. در این درس نیز همین مهارت به شما کمک می‌کند.

تعریف دنباله حسابی به زبان ریاضی: 

دنباله زیر را یک دنباله حسابی گویند.

. . . ,a, a+d, a+d+d, a+d+d+d

یا به صورت ساده شده ی زیر:

a, a+d, a+2d, a+3d

به زبان ساده می توان گفت اختلاف بین دو جمله متوالی ( پشت سر هم) همیشه ثابت است و برابر با d است که به آن قدر نسبت دنباله حسابی گفته می شود.

دقت کنید در آموزش دنباله های حسابی و هندسی پایه دهم مفاهیم را به صورت ملموس و با زبان ساده برای دانش آموزان توضیح دهید.

مثال: دنباله زیر را در نظر بگیرید.

…, 18, 14, 10, 6

ابتدا به سوالات زیر پاسخ دهید:

• آیا دنباله بالا یک دنباله حسابی است؟ چرا؟ 

جواب: بله. چون اختلاف جملات متوالی یک مقدار ثابت است. فاصله ی بین 6 و 10 برابر با 4 است. فاصله بین 14 و 10 برابر با 4 است و ….

• سپس قدر نسبت دنباله را به دست آورید.

جواب: با تفاضل دو جمله متوالی می توان مقدار قدر نسبت را به دست آورد. در نتیجه داریم 4=d.

• جمله عمومی دنباله را بنویسید.

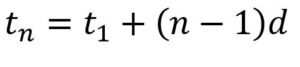
• مقدار 23 امین جمله دنباله را به دست آورید.

کافی است که در جمله عمومی به جای n مقدار 23 قرار دهیم تا مقدار جمله 23 ام به دست آید.

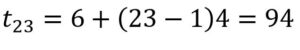
نکته: جمله nام یک دنباله حسابی با جمله اول t1  و قدر نسبت d به صورت

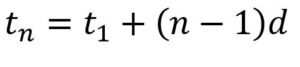نوشته می شود.

کار در کلاس 2 صفحه 22 کتاب ریاضی دهم:

• A و B دو شرکت عرضه کننده سیم کارت های تلفن همراه با شرایط زیرند:

       سیم کارت های شرکت A دارای هزینه ثابت 2000 تومان و هزینه هر دقیقه مکالمه 30 تومان

       سیم کارت های شرکت  B دارای هزینه ثابت 3000 تومان و هزینه هر دقیقه مکالمه 20 تومان

     فرض کنید an نشان دهنده هزینه کل n دقیقه مکالمه ماهانه از طریق سیم کارت شرکت A  و bn هزینه مشابه برای استفاده از سیم کارت شرکت B     باشد.

الف: مقدار an و bn را بر حسب n بنویسید.

ب: آیا an و bn هر کدام می توانند جمله عمومی یک دنباله حسابی باشند؟ چرا؟ 

بله. چون اختلاف جملات متوالی ثابت هست.

اگر جواب مثبت است، قدر نسبت هر یک را مشخص کنید. جواب: 30=da و 20=db

ث: سارا در هر ماه حدود یک ساعت و فاطمه ماهانه تقریبا 150 دقیقه با تلفن همراه مکالمه می کنند. به هر یک از آنها کدام سیم کارت را پیشنهاد می کیند؟ چرا؟

با توجه به محاسبه زیر به سارا پیشنهاد داده می شود که از سیم کارت شرکت A استفاده کند چون هزینه شرکت A برای سارا کمتر است.

برای فاطمه به عنوان تمرین انجام دهید.

تمرین دنباله های حسابی پایه دهم به سبک ریبازی

1. در جاهاهی خالی عبارت مناسب بنویسید.

• اختلاف بین …………… در دنباله های حسابی همیشه مقداری ثابت است. ( جواب: دو جمله متوالی)
• قدر نسبت d در یک دنباله حسابی برابر است با ………….. .( جواب: اختلاف دو جمله متوالی)
• جمله عمومی دنباله حسابی با جمله ی اول 3- و قدر نسبت 5 برابر است با : …………….. . (جواب: (3-)+(n-1)5)

• جمله ی دهم دنباله حسابی قسمت قبل برابر است با …………… . ( جواب: 42)

    2. واسطه حسابی را تعریف کنید. تعداد واسطه های حسابی بین دو عدد به چه چیزی بستگی دارد؟ (جواب: اعدادی که بین دو عدد قرار می گیرند و مجموعه اعداد را به دنباله حسابی تبدیل می کنند، واسطه حسابی نام دارند. به مقدار d بستگی دارد.)

با حل کار در کلاس 2  صفحه 23 کتاب جواب سوال 2 را توضیح می دهیم.

الف) بین 18 و 62 سه عدد را چنان قرار دهید که پنج عدد حاصل تشکیل دنباله حسابی بدهند. ( اعدادی که ما به دست می آوریم را واسطه حسابی می نامند.)

توضیح دهیم که با توجه به مساله قرار است جمله ی اول دنباله 18 و چون سه واسطه قرار می دهیم جمله پنجم برابر با 62 باشد.

جمله عمومی دنباله حسابی را می نویسیم و مقدار d را از آن به دست می آوریم.

 

 

پس دنباله به صورت زیر می باشد:

62, 51, 40, 29, 18

به اعداد 29، 40 و 51 واسطه های حسابی گویند.

سوال به سبک ریبازی و مفهومی برای آموزش دنباله های حسابی و هندسی پایه دهم: 

ب: بین عددهای ۱۸ و ۶۲ چند واسطه حسابی باید قرار دهیم تا دنبالهٔ تشکیل‌شده یک دنبالهٔ حسابی با قدر نسبت ۲ باشد؟

توضیح: اینجا مقدار d داده است و تعداد جملات را از ما می خواهد. ما می دانیم که جمله ی nام باید 62 باشد. پس جمله عمومی را می نویسیم و به جای جمله nام مقدار 62 قرار می دهیم و n را محاسبه می کنیم.

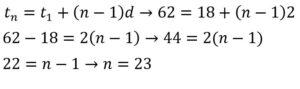
دقت کنید که تعداد جملات دنباله باید برابر با 23 باشد ولی چون تعداد واسطه ها را می خواهد، تعداد واسطه ها برابر است با 21=2-23.

حل تمرین 6 کتاب فصل دنباله های حسابی و هندسی پایه دهم صفحه 24:

• 100 قرص نان را بین ۵ مرد چنان تقسیم کنید که سهم های دریافت شده دنباله حسابی تشکیل دهد و یک سوم مجموع سه سهم بزرگتر، مساوی مجموع دو سهم کوچکتر باشد.

جواب: توضیح برای آموزش دنباله های حسابی و هندسی پایه دهم باید بسیار ساده و شفاف برای دانش آموزان با زبان ریاضی توضیح داده شود.

این جمله تمرین که “سهم های دریافت شده دنباله حسابی تشکیل دهد” یعنی اختلاف سهم نفر اول با نفر دوم برابر است با اختلاف سهم نفر دوم و نفر سوم یعنی فاصله بین سهم آنها ثابت است. نفر اول از همه کمتر و نفر پنجم از همه بیشتر سهم دریافت می کند.

این جمله تمرین که ” یک سوم مجموع سه سهم ِبزرگتر باید مساوی مجموع دو سهم باشد” یعنی :

ابتدا سهم سه نفر آخر را جمع کنیم تقسیم بر 3 کنیم ( ثلث مجموع سه نفر آخر)

سپس سهم دو نفر اول را با هم جمع کنیم ( مجموع سهم دو نفر اول )

حال بدانیم که ثلث مجموع  سه نفر باید بزرگتر مساوی مجموع دو نفر اول باشد.

بیا برویم و تمام این جملات را به صورت ریاضی بنویسیم:

ابتدا سهم نفر اول را a، نفر دوم را a+d، نفر سوم را a+2d، نفر چهارم را a+3d و نفر پنجم را a+4d تعریف می کنیم.

نکته : می دانیم که مجموع سهم این 5 نفر برابر با 100 است یعنی داریم: 5a+10d=100.

نکته: مجموع سهم دو نفر اول برابر است با : 2a+d  و ثلث مجموع سه نفر آخر برابر است با 3a+9d تقسیم بر 3 که می شود: a+3d

نکته: این دو باید با هم برابر باشند. یعنی 2a+d=a+3d که نتیجه می گیریم: a=2d

در ضمن داشتیم که 5a+10d=100 پس به جای a مقدار 2d قرار می دهیم و d را حساب می کنیم. لذا 10d=100  پس d=10  و a=20.

در پایان دنباله بابر است با :

30, 25, 20, 15, 10

دانش‌آموزانی که می‌خواهند دنباله های حسابی و هندسی پایه دهم را به‌خوبی یاد بگیرند، لازم است تک‌تک جملات این مطلب را با دقت بخوانند و با تمرکز کامل متوجه شوند که هر جمله چه نکته‌ای را بیان می‌کند. هنگامی که دانش‌آموز مفهوم هر بخش را عمیق و روشن بفهمد، نه‌تنها مباحث دنباله‌ها را به‌خوبی درک می‌کند، بلکه می‌تواند همه مسائل مرتبط را از ساده تا دشوار به‌راحتی و با اعتمادبه‌نفس حل کند. این شیوه مطالعه، یادگیری مفهومی و پایدار را تضمین می‌کند.

دانش‌آموزانی که دنباله های حسابی و هندسی پایه دهم را به‌خوبی درک کرده و مفاهیم ریاضی پایه را به‌طور کامل فرا گرفته باشند، می‌توانند مسائل مطرح‌شده در این مباحث را با تسلط و اطمینان حل کنند. چنین دانش‌آموزانی به دلیل فهم روشن فرمول‌ها، روابط و کاربردهای دنباله‌ها، قادرند مسائل ساده تا دشوار را به‌صورت منطقی، مرحله‌به‌مرحله و دقیق تحلیل کرده و به پاسخ درست برسند. این توانمندی نشان‌دهنده آن است که یادگیری پیوسته و اصولی، نقش مهمی در موفقیت در مباحث پیشرفته‌تر ریاضی دارد.

آموزش دنباله هندسی پایه دهم به سبک ریبازی 

قبل از تعریف دنباله هندسی ابتدا به تفاوت دنباله حسابی و هندسی می پردازیم تا این مفهوم را به خوبی یاد بگیریم.

دنباله حسابی می گوید هر جمله از اضافه شدن جمله قبلی با یک عدد ثابت به دست می آید که مقدار ثابت همان قدر نسبت d است که در قسمت بالا کامل توضیح داد شد.

به زبان ریاضی:

a2=a1+d ; a3=a2+d

ولی دنباله هندسی می گوید هر جمله از ضرب جمله قبلی در یک عدد ثابت به دست می آید. مثلا جمله اول را a1 در نظر بگیرید جمله دوم از ضرب جمله اول در یک عدد ثابت به دست می آید. جمله سوم از ضرب جمله دوم در همان عدد ثابت به دست می آید یعنی در دنباله هندسی داریم:

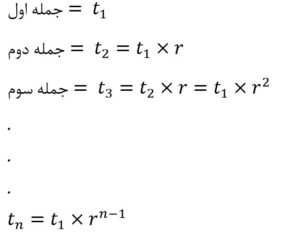
نمونه سوالات دنباله های هندسی:

مثال 1: دنبالهٔ زیر را در نظر بگیرید:

24, 12, 6, 3

الف) آیا این دنباله یک دنبالهٔ هندسی است؟ ( جواب: بله. چون هر جمله از ضرب جمله قبلی در 2 به دست آمده است.)
ب) اگر بله، قدر نسبت آن را تعیین کنید و جملهٔ دهم دنباله را بنویسید. ( جواب: قدر نسبت برابر با 2 است و جمله دهم برابر است با ضرب 3 در 2 به توان 9)

سوال: چگونه قدر نسبت دنباله هندسی به دست می آید؟ جواب: یکی از جمله های دنباله را بر جمله قبلی اش تقسیم می کنیم. مثلا  2= 3÷6

 

مثال 2: در یک دنبالهٔ هندسی، جملهٔ اول برابر ۵ و قدر نسبت برابر ۳ است. مجموع هفت جملهٔ اول را به دست آورید.

ابتدا نشان می دهیم که مجموع n جمله در دنباله هندسی چگونه به دست می آید:

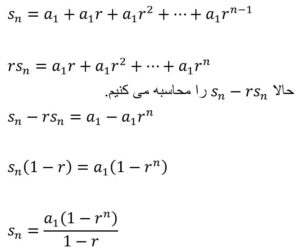
پس در مساله n=7 است. a1=5 و r=3 . با جایگذاری در فرمول بالا مقدار مجموع هفت جمله دنباله را به صورت زیر به دست می آوریم.

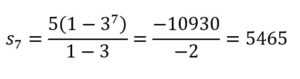
اکثر دانش‌آموزان مفاهیم ریاضی را به‌خوبی فرا نمی‌گیرند، زیرا زبان ریاضی در پایه‌های ابتدایی به‌صورت اصولی و کاربردی به آن‌ها آموزش داده نشده است. اگر والدین فرزندان خود را در کارگاه‌های ریبازی در دورهٔ ابتدایی شرکت دهند، این مشکل در پایه‌های بالاتر برطرف خواهد شد و یادگیری ریاضی برای آن‌ها بسیار آسان‌تر و لذت‌بخش‌تر می‌شود.

در آموزش دنباله های حسابی و هندسی پایه دهم، یک معلم باید توجه داشته باشد که پیوند مفاهیم جدید با مفاهیم قبلی نقش کلیدی در یادگیری دارد. بسیاری از دانش‌آموزان به این دلیل در یادگیری مفاهیم جدید دچار مشکل می‌شوند که مبانی و مفاهیم پیش‌نیاز را به‌خوبی درک نکرده‌اند. بنابراین، معلم باید قبل از ورود به مباحث جدید، مرور هدفمند و کوتاهی از مفاهیم قبلی ارائه دهد و نشان دهد که چگونه این مفاهیم با موضوعات جدید ارتباط پیدا می‌کنند.

نمونه سوالات دنباله های حسابی و هندسی پایه دهم ( سوالات تیزهوشانی )

1.در یک دنبالهٔ حسابی، جملهٔ سوم برابر ۱۲ و جملهٔ هشتم برابر ۲۷ است. قدر نسبت و جملهٔ اول را پیدا کنید. ( سطح سوال: متوسط)

2.بین دو عدد ۵ و ۴۱، چند واسطه حسابی باید قرار داد تا یک دنبالهٔ حسابی تشکیل شود که مجموع جمله‌های آن برابر ۲۷۶ شود؟ ( سطح سوال متوسط)

3. پنج عدد مثبت به‌صورت دنبالهٔ حسابی هستند. اگر مجموع سه جملهٔ وسط برابر ۴۵ و تفاوت جملهٔ آخر و جملهٔ اول برابر ۳۲ باشد، جمله‌ها را پیدا کنید. ( سطح سوال دشوار)

4. قرار است عددهای ۳ و ۶۳ را با درج تعدادی جملهٔ میانی به صورت یک دنبالهٔ حسابی درآوریم. به‌طوری‌که مجموع تمام جمله‌ها برابر ۲۵۸ شود.
الف) چند جملهٔ میانی ( واسطه حسابی) لازم است؟
ب) جملهٔ nام را بنویسید.

( سطح سوال دشوار)

5. مجموع پنج جملهٔ پیاپی یک دنبالهٔ حسابی برابر 85 است. همچنین مجموع مربعات همان پنج جمله برابر 1805 است. قدر نسبت و جملهٔ میانی را پیدا کنید. ( سطح سوال خیلی دشوار)

تمرینات مربوط به دنباله های هندسی:

1. در یک دنبالهٔ هندسی، جملهٔ سوم برابر 12 و جملهٔ پنجم برابر 108 است.
   الف) قدرنسبت دنباله را پیدا کنید.
   ب) جملهٔ اول دنباله را به دست آورید.
2. در یک مسابقه، بازیکنی در مرحلهٔ اول 5 امتیاز می‌گیرد و امتیازهای او تشکیل یک دنبالهٔ هندسی می‌دهند. اگر جمع سه مرحلهٔ اول برابر 35 باشد،
   الف) قدرنسبت را بیابید.
   ب) امتیاز مرحلهٔ سوم را پیدا کنید.
3. در یک دنبالهٔ هندسی، جملهٔ دوم برابر 6 است. اگر مجموع چهار جملهٔ اول برابر 30 باشد:
   الف) قدرنسبت را بیابید.
   ب) جملهٔ اول را پیدا کنید.
4. فرض کنید در یک دنبالهٔ هندسی با قدرنسبت مثبت، جملهٔ ششم 192 و جملهٔ سوم 24 است.
   الف) قدرنسبت را پیدا کنید.
   ب) مجموعهٔ هشت جملهٔ اول دنباله را محاسبه کنید.
5. در یک دنبالهٔ هندسی با قدرنسبت منفی، جملهٔ چهارم برابر 54- و مجموع پنج جملهٔ اول برابر 21 است.
   الف) جملهٔ اول را بیابید.
   ب) قدرنسبت را تعیین کنید.

یادگیری خود را از دنباله های حسابی و هندسی پایه دهم با پاسخ‌دادن به سؤال‌های طراحی‌شده در بالا ارزیابی کنید. این پرسش‌ها طوری تنظیم شده‌اند که هم میزان درک مفاهیم پایه را بسنجند و هم توانایی شما در حل مسائل متوسط و دشوار را محک بزنند. با حل آن‌ها می‌توانید متوجه شوید در کدام بخش‌ها تسلط کافی دارید و در کدام قسمت‌ها نیاز به مرور بیشتر احساس می‌شود.