آموزش شمارنده های اول و تجزیه عدد برای پایه هفتمی ها

در این مقاله به آموزش شمارنده های اول به وسیله مثالهای متناسب با مفاهیم کتاب پایه هفتم پرداختیم. تمام نکات مربوط به شمارنده های اول که در کتاب بیان شده است را به صورت مثالها و مسائل و  برای شما با زبان ریاضی توضیح داده شود.

شمارنده های اول یک عدد: 

تعریف شمارنده اول: شمارنده هایی از یک عدد که عدد اول هستند را شمارنده های اول آن عدد گویند.

مثال: شمارنده های اول عدد 24 را به دست آورید.

شمارنده های 24= 24، 12، 8، 6، 4، 3، 2، 1

از بین این شمارنده ها کدام یک عدد اول است؟ 2 و 3.

پس شمارنده های اول عدد 24 چه اعدادی هستند؟ 2 و 3

لذا می توان گفت که برای پیدا کردن شمارنده های اول یک عدد می توان روش هایی را بیان کرد که در ادامه به آن پرداخته شده است.

روش اول برای پیدا کردن شمارنده های اول یک عدد

به 2 روش می توانیم شمارنده های اول یک عدد را پیدا کنیم:

روش اول:

ابتدا شمارنده های آن عدد را می نویسیم. از بین شمارنده ها، دور اعداد اول را خط می کشیم. اعدادی که دورشان خط کشیدیم، شمارنده های اول آن عدد هستند.

مثال: شمارنده های اول 35 را بنویسید.

شمارنده های 35 را همگی نوشتیم. 1 عدد اول نیست. 35 هم عدد اول نیست ولی 5 و 7 هر دو عدد اول هستند. پس 5 و  7 را شمارنده های اول عدد 35 گویند.

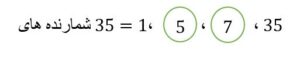
مثال: شمارنده های اول عدد 35 را بنویسید.

نکاتی که در مورد شمارنده های اول یک عدد باید بدانید:

• شمارنده اول یک اسم است و تعریف دارد. حواستان باشد که شمارنده دوم یا شمارنده سوم نداریم. فقط شمارنده های اول در ریاضی واژه تعریف شده اند.
• هر عدد طبیعی بزرگتر از 1 دارای حداقل 1 شمارنده اول است.

مثال: شمارنده های 20 را بنویسید و نشان دهید که حداقل یک شمارنده اول دارد. 

پاسخ:

شمارنده های 20 برابر است با : 1،2،4،5،10،20 . مشاهده می کنیم که عدد 20 دارای 2 شمارنده اول 2 و 5 است.

مثال:آیا 2 شمارنده اول دارد؟

پاسخ:شمارنده های 2 برابر است با 1و 2. چون 2 عدد اول است پس شمارنده اول 2 خود 2 است.

• هر عدد اول، فقط یک شمارنده اول دارد و آن خودش است.

مثال: 13 یک شمارنده اول دارد و خود 13 است.

مثال: 11 عدد اول است و یک شمارنده اول دارد و خود 11 است.

روش دوم برای پیدا کردن شمارنده های اول یک عدد 

برای پیدا کردن شمارنده اول یک عدد ابتدا باید آن عدد را با استفاده از نمودار درختی تجزیه کنیم.

نکات آموزشی تجزیه درختی برای پیدا کردن شمارنده های اول یک عدد:

1: ابتدا باید عدد داده شده را تجزیه کنیم.

تجزیه یک عدد : یعنی نوشتن یک عدد به صورت ضرب چندتا عدد. ولی وقتی تجزیه درختی کامل است که عدد را به صورت ضرب اعداد اول بنویسیم.

مثال: 6×6=36 یعنی 36 تجزیه شده است ولی کامل تجزیه نشده است.

مثال: عدد 36 را به صورت درختی تجزیه کنید. (به صورت ضرب اعداد اول نوشته شود.)

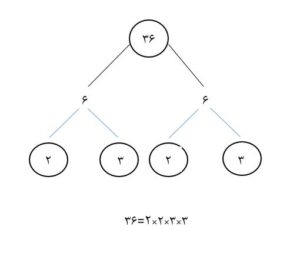
2. وقتی عدد را تجزیه کامل  کردیم، هر کدام از عددهای اول را که در تجزیه می بینیم، فقط یکبار می شماریم و تعداد شمارنده های اول عدد را می گوییم. فقط تکرار یک عدد اول در تجزیه عدد نباید باعث شود که تعداد شمارنده ها را بیشتر بگوییم.

مثال: عدد 36 چند شمارنده اول دارد؟ 

پاسخ: به تجزیه عدد 36 نگاه کنید. اعداد اول در تجزیه 2 و 3 هستند. پس 2 شمارنده اول دارد.

در تجزیه عدد 36 دقت کنید که 2 و 3 هر کدام 2 بار تکرار شدند ولی برای گفتن شمارنده های اول فقط یک بار شمرده می شوند. پس نباید بگویید که 36 دارای 4 شمارنده اول است بلکه باید بگویید 36 دارای 2 شمارنده اول است. شمارنده های اول عدد 36 عددهای 2 و 3 هستند.

مثال: عدد 12 چند شمارنده اول دارد؟

پاسخ: 12 را تجزیه می کنیم. 3×2×2=12. خوب دقت کنید که 12 هم دارای 2 شمارنده اول است. شمارنده های اول 12 اعداد 2 و 3 هستند. درست است که شمارنده اول 2 برای دوبار تکرار شده است ولی یک بار شمرده می شود.

تمرین: عددی دارای 3 شمارنده اول است. تجزیه عدد به صورت زیر است. آن عدد را بیابید.

• یکی از شمارنده های اول آن زوج است و 2 بار تکرار شده است.
• شمارنده ی اول دیگر آن بر 5 بخشپذیر است و فقط یک بار تکرار شده است.
• شمارنده اول دیگر مجموع دو شمارنده اول قبلی است و فقط یک بار تکرار شده است. 

پاسخ:

• تنها شمارنده اول زوج، عدد 2 است که 2 بار تکرار شده است یعنی در تجزیه 2 تا عدد 2 در هم ضرب شده اند.
• تنها شمارنده اولی که بر 5 بخشپذیر باشد خود 5 است.
• مجموع دو شمارنده برابر با 7 است که خود شمارنده اول است.

در نتیجه تجزیه به صورت زیر است: 7×5×2×2 یعنی عدد برابر با 140 است.

مثال: تجزیه عدد a برابر است با: 5×3×3×3×2=a. کدام جمله درست و کدام جمله نادرست است؟ جملات نادرست را اصلاح کنید.

الف: a دارای 5 شمارنده اول است. جمله نادرست است چون a دارای سه شمارنده اول (2،3 و 5) است.

ب: 27 شمارنده a است. جمله درست است چون از ضرب شمارنده های اول در یکدیگر شمارنده های عدد را می توانیم پیدا کنیم. 27=3×3×3

ج: اعداد 6، 10، 18 و 33 شمارنده های a هستند. جمله نادرست است. چون 33 از ضرب هیچ کدام از شمارنده ها به دست نمی آید.

د: a مضرب عدد 90 است. جمله درست است. چون 90=5×3×3×2 پس 90 شمارنده a است لذا a مضرب 90 است.

مثال:سه عدد بنویسید که تعداد شمارنده های اول آنها یکسان باشد.

پاسخ:

مرحله اول: چندتا شمارنده اول را انتخاب کنید. مثلا 2 و 3

مرحله دوم: هر دفعه یک ضربی با عددهای 2 و 3 بسازید فقط تعداد عددهای 2 و 3 را در ضرب تغییر دهید. 6=3×2؛ 12=3×2×2؛ 24=3×2×2×2؛

سوال: شمارنده های اول اعداد 6، 12 و 24 را بنویسید. آیا تعداد آنها یکسان است؟

پاسخ: 2 و 3.  بله. هر سه عدد، شمارنده های اول یکسانی دارند.

سوال: آیا شمارنده های اعداد 6، 12 و 24 یکسان است؟

پاسخ: نه . چون 8 شمارنده 24 است ولی شمارنده 6 و 12 نیست. ( چطوری از ضرب نوشته شده برای 24 متوجه شدیم که 8 شمارنده 24 است؟)

سوال: با راهبرد الگوسازی شمارنده های عدد 100 را بیابید.

پاسخ:

مرحله اول: عدد 100 را تجزیه کنید. تجزیه 100 به این صورت است: 5×5×2×2=100

مرحله دوم : نوشتن عدد 1. ( چون 1 شمارنده هر عددی است.)

مرحله سوم: نوشتن شمارنده های اول که در تجزیه می بینیم: 2 و 5

مرحله چهارم: عددهایی که از ضرب فقط دو شمارنده اول داخل تجزیه به دست می آیند را می نویسیم. 

ضربهایی که با 2 شمارنده اول داخل تجزیه می توانیم بنویسیم، به این صورت است: 2×2؛ 5×2؛ 5×2؛ 5×2؛ 5×2؛ 5×5.

چه اعدادی از این ضرب به دست می آیند؟ 4، 10 و 25. این 3 عدد شمارنده های دیگر 100 هستند.

مرحله پنجم: عددهایی که از ضرب سه شمارنده اول داخل تجزیه به دست می آیند را می نویسیم.

ضربهایی که با سه شمارنده اول داخل تجزیه می توانیم بنویسیم، به این صورت است: 5×2×2؛ 5×2×2؛ 5×5×2؛

چه اعدادی از این ضربها به دست می آیند: 20 و 50

مرحله ششم: عددهایی که از ضرب 4 شمارنده اول داخل تجزیه به دست می آیند را می نویسیم.

ضرب چهار شمارنده اول داخل تجزیه مثل خود تجزیه می شود. وقتی در نوشتن ضرب ها به خود تجزیه رسیدیم، یعنی تمام شمارنده ها نوشته شده است:

مرحله آخر: نوشتن تمام عددهایی که در هر مرحله به دست آمده است را می نویسیم تا تمام شمارنده ها را نوشته باشیم و سپس از کوچک به بزرگ مرتب می کنیم:1، 2، 5، 4، 10، 25، 20، 50 و 100 پس این عددها را مرتب می کنیم: 100، 50، 25، 20، 10، 5، 4، 2، 1

کاربرد تجزیه اعداد به صورت حاصل ضرب شمارنده های اول 

• ساده کردن کسرها

یکی از کاربردهای تجزیه اعداد، ساده کردن کسرها است.

جالب است که اگر تجزیه صورت و تجزیه مخرج یک کسر را بنویسیم و کسر را ساده کنیم، آن گاه کسر به ساده ترین شکل ممکن نوشته می شود و دیگر نمی توان آن کسر را ساده تر کرد.

مثال: کسر زیر را با روش دوره دبستان تجزیه کنید.

ابتدا صورت و مخرج بر 4 تقسیم شده است و در مرحله بعدی صورت و مخرج هر دو بر 3 تقسیم شده اند و کسر به ساده ترین شکل ممکن نوشته شده است.

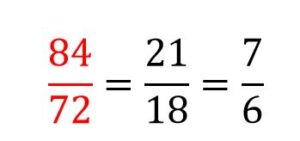
حالا بیاییم و با استفاده از تجزیه صورت و مخرج ساده کنیم.

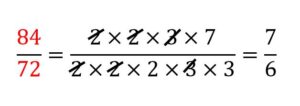
نکته: شاید دانش آموزی بگوید: کسر اول که راحت تر ساده شد چرا از روش تجزیه استفاده کنیم. به دلایل زیر روش تجزیه مناسب تر است:

1. در روش دوم نباید بررسی کنیم که صورت و مخرج را بر چه اعدادی می توانیم تقسیم کنیم. ( مثلا 84 و 72 هر دو باید بدانیم که بر 4 بخشپذیر هستند و سپس 21 و 18 هر دو بر 3 بخشپذیر هستند.)

2. از طرفی اعداد که بزرگ باشد روش تجزیه بسیار راحت تر است:

• چون ما فقط تجزیه می کنیم
• و سپس عامل های اول مشترک در صورت و مخرج را با هم ساده می کنیم.

تمرین: یک کسر مثال بزنید که صورت آن یک عدد 4 رقمی و مخرج آن یک عدد 3 رقمی باشد و اصلا نتوانیم آن را ساده کنیم.

شمارنده های اول و مثالی از نمونه سوال کتاب ریاضی پایه هفتم 

1: مساحت یک زمین مستطیلی شکل که طول و عرض آن عدد طبیعی هستند، برابر با 24 متر مربع شده است.

الف: تمام حالت هایی که طول و عرض مستطیل می تواند داشته باشد را بنویسید. 

ب: طول و عرض مستطیل چه ارتباطی با مساحت مستطیل دارند؟

پاسخ الف:

نکات: ابتدا باید فرمول مساحت مستطیل را به خاطر بیاوریم که برابر است با طول × عرض.

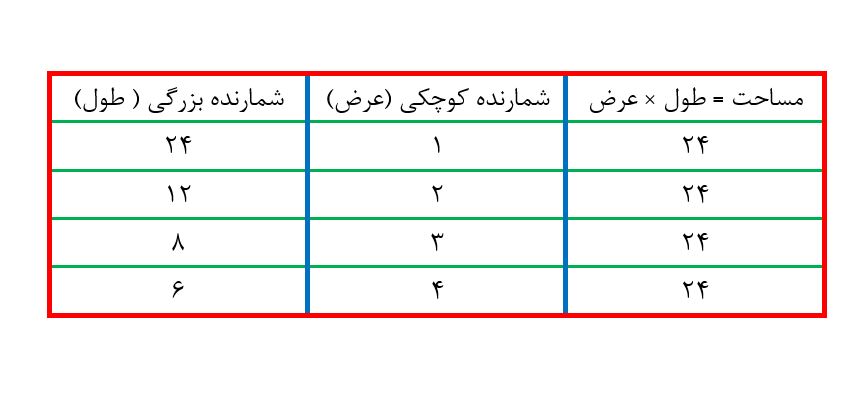
پس کافی است شمارنده های 24 را بنویسیم و هر کدام از جفت شمارنده ها را طول و عرض در نظر بگیریم. ( البته شمارنده بزرگی را طول و شمارنده کوچکی را عرض می نامیم.

شمارنده های 24 برابر است با: 24، 12، 8، 6، 4، 3، 2، 1

در نتیجه جدول زیر را داریم:

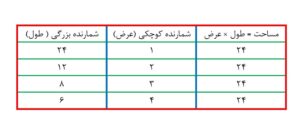
جدول نشان می دهد که زمین می تواند طول 24 و عرض 1 داشته باشد یا طول 12 و عرض 2 متر داشته باشد و …

پاسخ ب:

مشخص است که طول و عرض مستطیل شمارنده های مساحت هستند.